フィボナッチ数列

相場でも38.2戻しとか61.8戻しといったりして反転ポイントになったり相場以外でも黄金比とか平均律とか呼ばれているフィボナッチ数列の比率。なぜその数字かっていうのがわからずに漠然と数字だけ覚えてるだけなのでここで少しお勉強してみようと思います。

フィボナッチ数列

上の数列がフィボナッチ数列です。レオナルド・フィボナッチが13世紀に再発見(※古代ギリシャやエジプトの数学者には以前から知られていた)した数列です。この数列にはいくつかの面白い特徴があります。

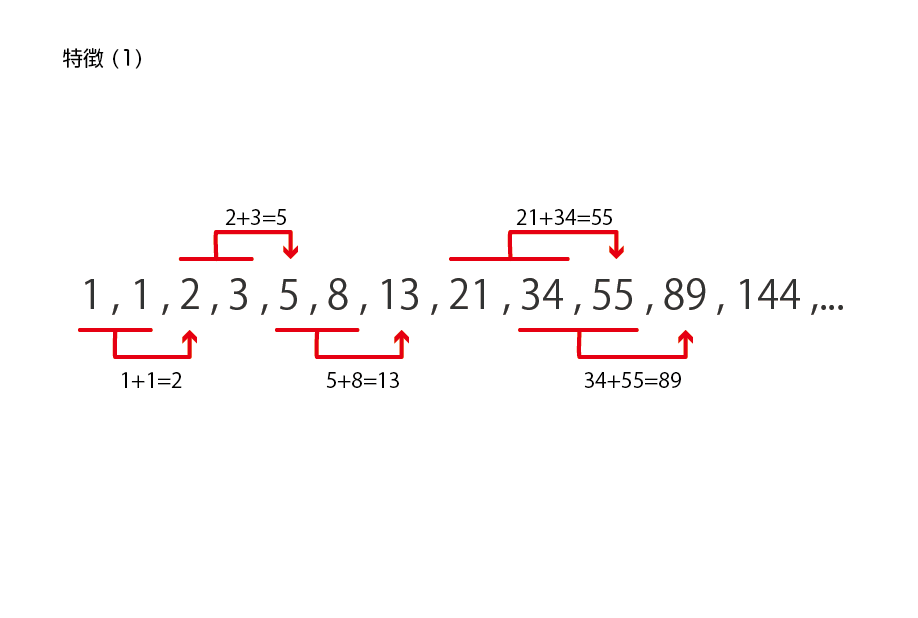
特徴1 : (An+2) = (An) + (An+1)

2つの連続する数字の合計は次の数に一致します。例えば6番目の「8」は4番目の「3」と5番目の「5」を足した数になります。

特徴2 : (An) ÷ (An+1) ≒ 0.618

ある数の次の数に対する比率は数列が進むごとに0.618に近づいていきます。面白いですよね。特に7番目以降は振れ幅も小さくなりほぼ0.618に近似できます。

特徴3 : (An+1) ÷ (An) ≒ 1.618

ある数の前の数に対する比率は数列が進むごとに1.618に近づいていく。これは先の特徴2の逆数です。割る数と割られる数を反対にしただけ。

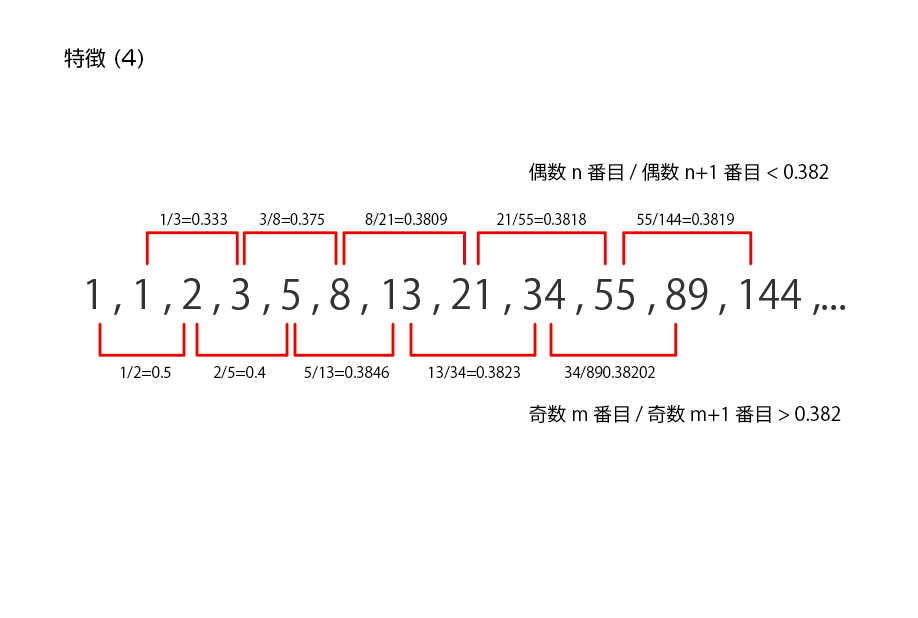
特徴4 : (An) ÷ (An+2) ≒ 0.382

1つおきの数字どうしの比率は0.382に近づいていく。これも特徴2、３と同様に逆に割れば2.618に近づいていく。

代表的な特徴は以上の4つ(5つ)です。

歴史上の利用

以前からこの数列は黄金比とか平均律と呼ばれる比率で音楽・美術・建築・生物学に応用されてきました。ギリシャ人はこの黄金比をパルテノン神殿の建設に利用したりまた、エジプトではギザの大ピラミッドに利用されたりもしています。カタツムリの殻の渦巻きとか人間の耳もこの比率になってるとか。フィボナッチ数列の関係が自然界や人間の行動に広く見受けられます。

相場でも戻しの比率やブレイクターゲット、エリオット波動にも利用されているのでこの比率は頭に入れておきたいところです。